二叉排序树-白红宇

二叉排序树又称二叉查找树，它是一种对排序和查找都很有用的特殊二叉树。

定义：

（1）若它的左子树不为空，则左子树上的所有结点的值均小于它的根结点的值；

（2）若它的右子树不为空，则右子树上所有结点的值均小于它的根结点上的值；

（3）它的左右子树本身也分别为二叉排序树。

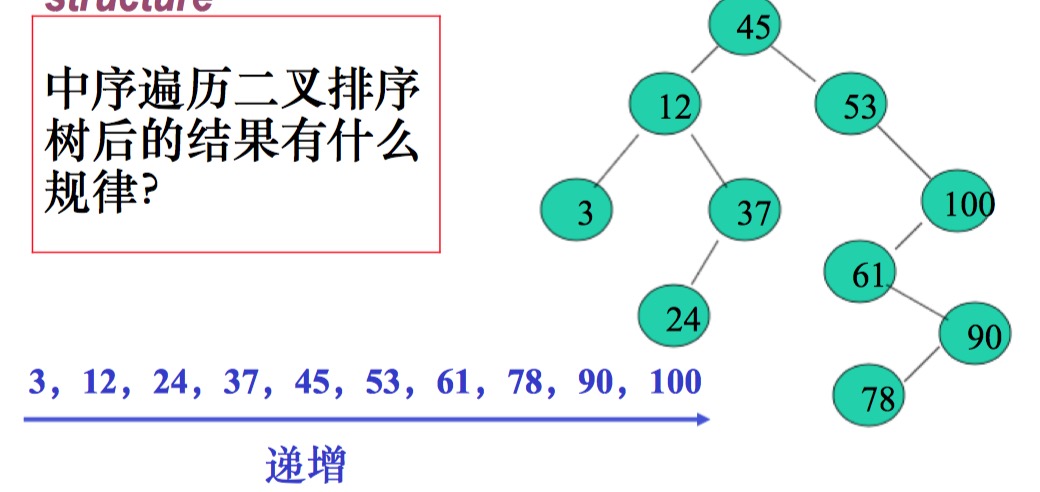
这里写图片描述

通过中序排列我们发现中序遍历的结果是结点的值是由低到高的。

二叉排序树的二叉链表存储表示

typedef struct{  keyType key；  InfoType other info；}ElemType；typedef struct BSTNode{ ElemType data； struct BSTNode *lchild，*rchild；}BSTNode，*BSTreet；

二叉排序树的查找

二叉排序树的查找依然沿用前面介绍的顺序查找和折半查找。

递归查找

（1）若二叉排序树为空，则查找失败，则返回空指针。

（2）若二叉排序树非空，将给定值key与根结点的关键字T->data.Key进行比较：

若key等于T->data.key,则查找成功，返回根结点地址；

若key小于T->data.key，则进一步查找左子树；

若key大于T->data.key，则进一步查找右子树。

算法描述

BSTree SearchBST(BSTree T,KeyType key)     {            //在根指针T所指二叉排序树种递归地查找某个关键字等于key的数据元素            //若查找成功，则返回指向该数据元素结点的指针，否则返回空指针            if((!T)||key==T->data.key) return T;    //查找结束            else if(key
     
      data.key) return SearchBST(T->child,key);//在左子树上继续查找        else return SearchBST(T->child,key);//在右子树上继续查找    }

二叉排序的插入

（1）若二叉排序树为空，则待插入结点*S作为根结点插入到空树中。

（2）若二叉排序树非空，则将key与根结点的关键字T->data.Key进行比较：

若key等于T->data.key，则停止插入；

若key小于T->data.key,则将*S插入左子树；

若key大于T->data.key,，则将*S插入右子树。

这里写图片描述

/*  当二叉排序树T中不存在关键字等于key的数据元素时， *//*  插入key并返回TRUE，否则返回FALSE */Status InsertBST(BiTree *T, int key) {      BiTree p,s;if (!SearchBST(*T, key, NULL, &p)) /* 查找不成功 */{    s = (BiTree)malloc(sizeof(BiTNode));    s->data = key;      s->lchild = s->rchild = NULL;          if (!p)         *T = s;            /*  插入s为新的根结点 */    else if (key
       
        data)         p->lchild = s;    /*  插入s为左孩子 */    else     p->rchild = s;  /*  插入s为右孩子 */return TRUE;} else return FALSE;  /*  树中已有关键字相同的结点，不再插入 */}

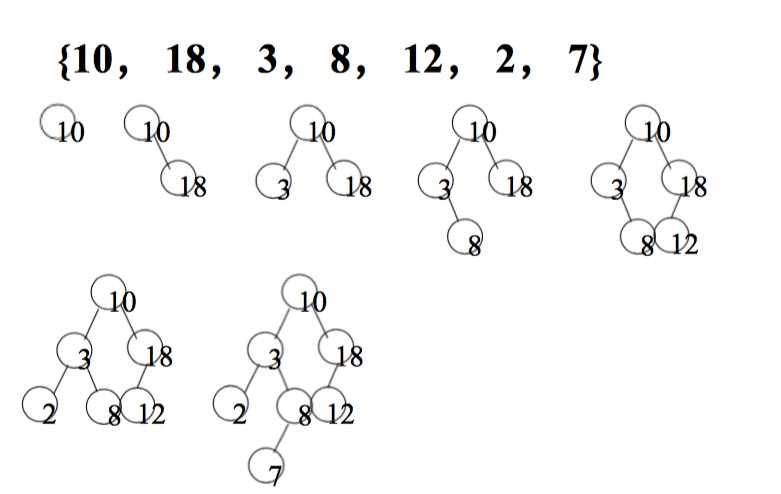
二叉排序树的创建

二叉排序树的创建是从空的二叉排序树开始，每输入一个结点，经过查找操作，将新结点插入到当前二叉排序树的合适位置。

（1）将二叉排序树T初始化为空树

（2）读入一个关键字为key的结点，将此结点插入二叉排序树T中。

（3）重复操作，直至读入的关键字key是输入结束标志。

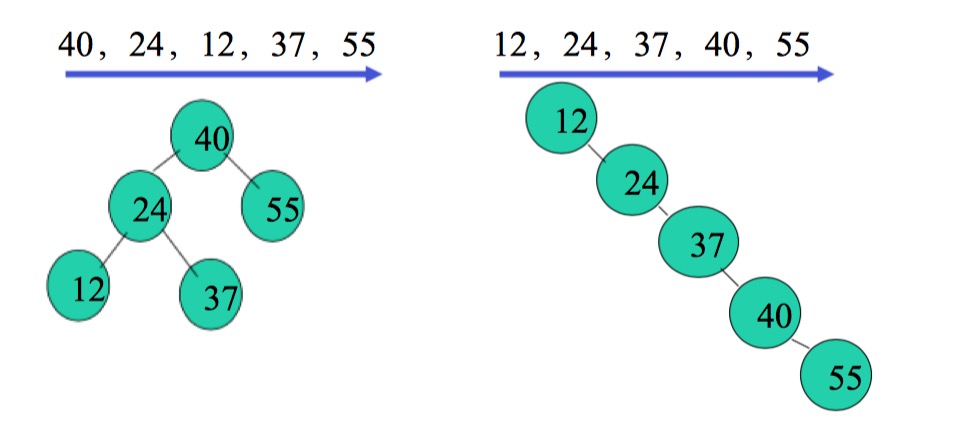
Void CreatBST(BSTree &T){T=NULL;cin>>e;while(e.key!=ENDFLAG){ InsertBST(T,e); cin>>e;}}

这里写图片描述

注意:不同的的插入次序的序列生成不同形态的二叉排序树

这里写图片描述

二叉排序树的删除

在二叉排序树中删除一个结点，这是二叉排序树中最有深度的操作。

主要分三种操作：

若*p结点为叶子结点，即PL(左子树)和PR(右子树)均为空树。由于删去叶子结点不破坏整棵树的结构，则只需修改其双亲结点的指针即可。

若*p结点只有左子树PL或右子树PR，此时只要令PL或PR直接成为其双亲结点*f的左子树（当*p是左子树）或右子树（当*p是右子树）即可，作此修改也不破坏二叉排序树的特性。

若*p结点的左子树和右子树均不空。在删去*p之后，为保持其它元素之间的相对位置不变，可按中序遍历保持有序进行调整。比较好的做法是，找到*p的直接前驱（或直接后继）*s，用*s来替换结点*p，然后再删除结点*s。

/* 若二叉排序树T中存在关键字等于key的数据元素时，则删除该数据元素结点, */

/* 并返回TRUE；否则返回FALSE。 */

Status DeleteBST(BiTree *T,int key){         if(!*T) /* 不存在关键字等于key的数据元素 */ return FALSE;else    {if (key==(*T)->data) /* 找到关键字等于key的数据元素 */     return Delete(T);else if (key<(*T)->data)    return DeleteBST(&(*T)->lchild,key);else    return DeleteBST(&(*T)->rchild,key);}}/* 从二叉排序树中删除结点p，并重接它的左或右子树。 */Status Delete(BiTree *p){BiTree q,s;if((*p)->rchild==NULL) /* 右子树空则只需重接它的左子树（待删结点是叶子也走此分支) */{q=*p; *p=(*p)->lchild; free(q);}else if((*p)->lchild==NULL) /* 只需重接它的右子树 */{    q=*p; *p=(*p)->rchild; free(q);}else /* 左右子树均不空 */{q=*p; s=(*p)->lchild;while(s->rchild) /* 转左，然后向右到尽头（找待删结点的前驱） */{    q=s;    s=s->rchild;}(*p)->data=s->data; /*  s指向被删结点的直接前驱（将被删结点前驱的值取代被删结点的值） */if(q!=*p)    q->rchild=s->lchild; /*  重接q的右子树 */ else    q->lchild=s->lchild; /*  重接q的左子树 */free(s);}return TRUE;}

性能分析

二叉排序树的查找长度与二叉树的形态有关，即

最好：log2n（形态均匀，与二分查找的判定树相似）

最坏：（n+1）/2（单支数）

改善：

所以为了改善查找效率就引入我们接下来要学习的一种更优良的树—-平衡二叉树